Avoiding the MSVCR100.dll, MSVCP100D.dll, or MSVCR100D.dll is missing error (Also MSVCR110.dll, MSVCR120.dll, MSVCR140.dll)
Note: This also applies to newer MSVCR110.dll, MSVCR120.dll and MSVCR140.dll.
MSVCR100.dll
This msvcr100.dll is the Microsoft Visual C++ Redistributable dll that is needed for projects built with Visual Studio 2010. The dll letters spell this out.
MS = Microsoft
V = Visual
C = C program language
R = Run-time
100 = Version
If you create a C++ project in Visual Studio 2010, this file is probably needed.
MSVCP100.dll
This msvcp100.dll is the Microsoft Visual C++ Redistributable dll that is needed for projects built with Visual Studio 2010. The dll letters spell this out.
MS = Microsoft
V = Visual
CP = C++
100 = version
If you create a C++ project in Visual Studio 2010, this file is probably needed.
MSVCR100D.dll
The MSVCR100D.dll is almost the exact same file only the D at the end stands for Debug. This file has debugging enabled and is not considered redistributable.
Why the error?
Ok, so recently I switched to Visual Studio 2010. I had a C++ application that worked perfectly in Visual Studio 2008. Once I compiled it with Visual Studio 2010 and ran it on a clean 2008 server (fully patched but otherwise clean), it failed to run with the following error.
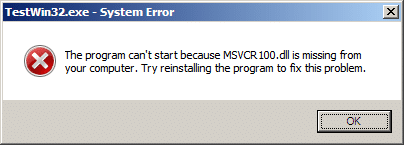
TestWin32.exe – System Error
The program can’t start because MSVCR100.dll is missing from your computer. Try reinstalling the program to fix this problem.
Here is the screen shot:
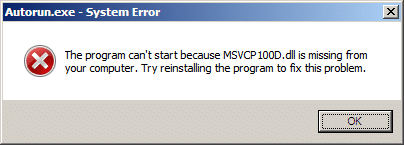
The same things happens with the debug version of the file, only it is a the debug version of the same DLL as noted by the fact that the DLL name ends with D.
Autorun – System Error
The program can’t start because MSVCR100.dll is missing from your computer. Try reinstalling the program to fix this problem.
The screen shot is identical except for the D in the dll name.
I create a new project in Visual Studio 2010 using the project type of C++ Win32 Project and without making a single change to the default project, I built the file and tested it on my clean machine and the same issue occurred.
So obviously that is not acceptable. It seems like this should just not happen by default, but unfortunately it does.
Solution
It was actually really easy to resolve for my one project.
Here is what I did.
You can solve this any of the following ways:
- Statically link to the dll files so they are compiled into my executable instead of referenced as separate dll files.
- Included the dll in the same directory as the exe (I actually didn’t try this but I assume it would work).
- Forced everyone to install the VC++ Runtime Redistributable before running the app.
The first option seems the most stable and robust and easiest for a single executable. So that is the one I am going to use.
The second option doesn’t really make sense to me and I would probably never do it. Maybe if I had dozens of executable files that all required the same DLL and I didn’t have an installer, and I wanted to conserve size, which probably wouldn’t happen for me since I am pretty good at creating a quick installer. Though you might be in this a situation.
The third option would make sense if I was planning on running my executable after an install. During the install I could include the VC++ Runtime Redistributable and all would be fine.
Statically Linking the DLLs
Make sure you resolve it for both Release and Debug. The steps are slightly different.
Release
- In Visual Studio, I went to the project Properties.
- I changed my Configuration to Release.
- I went under Configuration Properties | C/C++ | Code Generation
- Look at the Runtime Library setting. It is set to this: Multi-threaded DLL (/MD)
Change it to this: Multi-threaded (/MT) - Rebuild.
Debug
Almost exactly the same as release.
- In Visual Studio, I went to the project Properties.
- I changed my Configuration to Debug.
- I went under Configuration Properties | C/C++ | Code Generation
- Look at the Runtime Library setting. It is set to this: Multi-threaded Debug DLL (/MDd)
Change it to this: Multi-threaded Debug (/MTd) - Rebuild the debug
It might be a good idea for me to figure out how to change the project so when I create a new project of this type, those settings are the default.
Install the VC++ Runtime Redistributable
Release
Download the appropriate version of VC++ Runtime Redistributable:
| File Version | VC++ Runtime Version |
|---|---|
| MSVCR100.dll | Microsoft Visual C++ 2010 Redistributable Package (x86) |
| MSVCR110.dll | Microsoft Visual C++ 2012 Redistributable Package (x86) |
| MSVCR120.dll | Microsoft Visual C++ 2013 Redistributable Package (x86) |
| MSVCR140.dll | Microsoft Visual C++ 2015 Redistributable Package (x86) |
Just google these and you will find the download links. Install the correct version and you are good to go.
Debug
If you are missing MSVCR100D.dll, then that is a debug dll and is not part of the free to download Visual C++ Redistributable package. So you pretty much are stuck with copying it from your dev box. Copy it to the C:\Windows\System32 directory. You need admin privileges to do this.
Note: You would never want to redistribute the debug dll anyway.


%%
Also visit my site ... cbd Hemp flowers & hash
%%
Review my blog post: cbd hash online
%%
Look at my blog post; Seo services Price
whoah this blog is wonderful i really like reading your articles. Keep up the great paintings! You realize, a lot of people are hunting round for this info, you could help them greatly.
barbie movie collection torrent download
Avoiding the MSVCR100.dll, MSVCP100.dll, or MSVCR100D.dll is missing error | Rhyous
how to install kodi 15.1 on apple tv
Avoiding the MSVCR100.dll, MSVCP100.dll, or MSVCR100D.dll is missing error | Rhyous
resume format for experienced free download
Avoiding the MSVCR100.dll, MSVCP100.dll, or MSVCR100D.dll is missing error | Rhyous
john lewis song 2012
Avoiding the MSVCR100.dll, MSVCP100.dll, or MSVCR100D.dll is missing error | Rhyous
www.yjbct.cn
Avoiding the MSVCR100.dll, MSVCP100.dll, or MSVCR100D.dll is missing error | Rhyous
real follows
Avoiding the MSVCR100.dll, MSVCP100.dll, or MSVCR100D.dll is missing error | Rhyous
exact hosting
Avoiding the MSVCR100.dll, MSVCP100.dll, or MSVCR100D.dll is missing error | Rhyous
re: second option doesn’t really make sense to me
This is called "side-by-side deployment" and is intended for the case where you have need for a specific version of a DLL, but do not want to force the user to install the entire package that contains the one DLL you need.
Using this side-by-side deployment, different programs you deploy can have different versions of the same DLL without conflict.
Or, conversely, you can deploy different versions of the same program in different directories, and each version of your program gets the correct version of support DLL.
-Jesse
Works like a charm ! Thanks !
You helped me too.
I new I needed to switch from DLLs to static linking but I believed the option to be found under the Linker node. Only after reading your article I realized the use of a run-tume linked DLL requires additional code such as calls to LoadLibrary(), GetProcAddress(), FreeLibrary().
Thank you very much.
Just wanted to say you a big THANKS!
Greetings!
icecreamthebook.com
Avoiding the MSVCR100.dll, MSVCP100.dll, or MSVCR100D.dll is missing error | Rhyous
Thanks, it's really work
Is there any solution to link the dll's to a CLR project?
Thanks, Thanks you very much...
You saved me!!!! Thanx much! This is working solution!
Thanks so much for this solution! You saved me tons of time 🙂
This is a very lackluster and undeveloped feature of the game, and brings the multiplayer experience down a little.
Sony will start sending emails out to all customers shortly
with details on how to sign-up for the program. Nothing has been confirmed, and it appears that
this service, if it is indeed in development, will not be available until at least 2013.
Hello,
I've to use Common Language Runtime Support '/clr' to compile my dll.
However, '/clr' and '/MT' options are incompatible so i can't change to Multi-threaded (/MT).
Do you have any solutions ?
Thks,
LOL. Looks like you didn't take time to read the solution. Only the first of the three solutions listed requires you to statically link the DLLs. Look at solution 2 or 3.
thanks for the solution.. but i still can't solve it.
I use VC++2008 instead of 2010. I tried using the 3rd solution. But, after I install Visual C++ 2008 Redistributable Package (x86), the missing msvcp100.dll still occured. help plz..?
If it is saying you are missing msvcp100.dll, then you need the vc++2010. The vc++2008 installs msvcr90.dll which would not be the right one.
Hi Rhyous,
Alternatively you can run a patch "vcredist_x86.exe" which you can get from the following link.
http://www.microsoft.com/en-us/download/details.aspx?id=5555
Mahendra varman, you realize that is solution #3, right? And it is not a patch. A patch is something different.
Thanks alot for this. Kept having this issue when compiling dbgen and your steps solved it!
Hallo,
thanks a lot for this help!!!
Thank you.
But your suggestion of statical linking does not work.
In VS 2010, I selected /MT for Code Generation in 64 bit release DLL and rebuilt. Size increased (from 32K to 93K). But Dependency Walker still shows MSVCR100.DLL as used.
Currently, did not find a way to link without this DLL.
So, had to search another ways.
Force Redistributable setup - problems to detect whether already installed, a lot of GUIDs for different versions. And I have also VM which have msvcr100 without Redistributable installed.
So, my current solution in Setup - try to load msvcr100.dll. If fails, redistribute it in Program Files.
Sorry, /MT really does the work.
There was a problem with Dependency Walker data refresh - it continued erroneously show msvcr100 in dependencies.
Thanks a lot, saved a lot of time.
Just having to figure out where C/C++ node is in VS2010 was troublesome. I had to add a dummy cpp file (and then I deleted it) to view the node in the configuration properties (whereas my project already include cpp files...).
Thanks for sharing the information. It worked like charm for me.
When I first met the problem some days ago, I used [dumpbin.exe /depends appname.exe] to get the needed libraries for my application then thought about get msvcr100d.dll from the internet.
Secondly, I realised that the static linking process described resulted in increase in application size. Mine rose from 90Kb to 453Kb.
Anyway, thanks a lot.
Yes, you either have to increase size by including the vcredist installer, or add the dlls to your own installer, or static link. They all increase size just in different ways. There is no way to avoid increased size in one way or the other.
I installed VC++2010 redist before installing the WAMP server and this worked perfectly for me. Thanks a bunch!
Thanks ! This Problem Solve......
i really thank dis post!!!! step 3 is working thanks again
i really thanks dis post!!!! step 3 is working thanks again
Just another thanks! I really needed this. To bad Microsoft make this so hard to figure out.
Thank you!
Precisely what I was looking for 🙂
dear sir 1st option working thank you .
I hv a same problem in downloading WAMP server in Windows 7.What i do????????
Thanks,
First option worked.
Thanks dude 1st option works perfectly.... 🙂
It worked for me. Thanks a ton.
Thanks a lot! Third option worked perfectly.
Just for others who run into the same issue:
I was able to get past the error using several methods above, static link, moving the .dll in with the package,
etc. Now I get a "The application was unable to start correctly (0xc000007b)" error.
Honestly Microsoft, just kill off the .dll nonsense already. Its a nightmare, it causes way more problems than it
was ever designed to solve, and nobody (but nobody) needs to save memory the way dlls were designed to do.
Scott
So the follow up is that installing visual studio on the target machine fixed the issue. This solution
really stinks, but it is good enough for right now. Note that both the machine used to generate the
application and the target (which is one foot away) are both running windows 7 64 bit. None of the
other solutions worked.
Scott
For those who get the same "unable to start correctly" error, it probably means that you copied the wrong .dll . For 64-bit applications, you have to copy the dll from "C:\Windows\SysWOW64" instead of "C:\Windows\System32".
Also, note that sometimes you need more than "msvcr100d.dll", the next error could be for "msvcp100d.dll", and that means that you got the first file ("msvcr100d.dll") right.
Had this same issue. Apparently I "did it right", because then I got the msvcp100d.dll error.
Installed only Windows 64 Redistributable before, went through and installed the x86 Redistributable, and it all works good now.
Thanks for the help!
Thanks !
Great advice, worked for me the first time. Thanks!!
if you give a download link for this dll , would be great , i cant found it.
You don't download the dll alone, you download the Microsoft Visual C++ Redistributable installer.
http://www.microsoft.com/download/en/details.aspx?id=5555
thanks this worked for me.
you rock! the 3rd option worked
Thanks a zillion
הודעה זו מופיעה פעמים רבות וברצוני לבטלה!!!
I had the same error message and just un-installed Google Chrome, then re-installed it. It is now working just fine.
Great!
I got stuck with this problem and your post gave me the solution.
Thankls a lot for sharing your knowledge.
Regards.
I get this error.... but don't have Visual Studio.... The only thing I can think of is that a co-worker sent me a presentation video recently and I've been receiving this message ever since.... Thoughts on how to fix it?
Try solution 3, install the Microsoft Visual C++ 2010 Redistributable Package. It is downloadable from Microsoft's web site.
thanks for the support its working fine ..
Thank you - that was a nice quick fix!
[...] I am not going to explain the solution again here, because it is all documented here: Avoiding the MSVCR100.dll or MSVCR100D.dll is missing error [...]
Thanx... I have tested ur 2nd option too it also works fine .cheers
Oh my gosh, I wish I found you 3 weeks ago.... What a small and stupid setting change that worked! You are the man, thank you so much. Also, I really appreciate the walk through too often people assume that you will know exactly what buttons to click. I wish everyone on the internet could answer questions this easily. As a side note, I will never understand why Microsoft assumes that just because I know how to write a program that I will know every single compiler setting to get the program ready for release.
Save my ass big time. Thank you from Washington DC.
Little question, I do got the files etc, but I get: Can't find accespoint off the procedure ??1critcal_section@Concurreny@@QAE@XZ in the DDl-file MSVCR100.dll
Rebuilding with static libraries in some cases causes:
LIBCMT.lib(crt0.obj) : error LNK2019: unresolved external symbol _main
Others suggest this is due to functions that rely on CRT initialization (e.g. strcmp), no clear answer found. (Nothing to do with ATL in my case.)
Any suggestions?
Not sure, I haven't seen that issue.
Ah cheers man, very clean and easy to follow walk through.
Much thanks 🙂
Thanks a lot. This one was very very helpful...
http://www.dll4free.com/msvcr100.dll.html
Whoa! This article saved me loads of irritations (and boy, did I already swallow loads of 'em!).
You saved ny butt! Loads of thanks 'cos you're a boy, if you were a girl ....
Glad to be of help!
THANKS A LOT! U SAVED ME!
'/clr' and '/MTd' command-line options are incompatible
i get that error every time i try to debug.
I also get this problem, I have been trying to statically link msvcr100d into my program but I get the message "Command line error D8016: '/clr' and '/MTd' command-line options are incompatible" and can't use No common language runtime support.
You're a life saver. Thank you!
Thanks for this man it helped me a lot
Thanks so much. I appreciate not only the steps to fix the problem, but also the explanation of what the file is and other potential solutions! Well written.
O-M-G.
Thanks so much!
thanks - exactly this fixed my problem
thank you very much
Thank You, this is exactly what I needed to fix my problem!
Make sure if your running VS2010 (with SP1) installed - that you have the right redist
http://www.microsoft.com/downloads/en/details.aspx?FamilyID=6201A933-4806-4036-8895-A340D7BEBF10&%3Bdisplaylang=en
At present - its in beta...
Ahm... What`s the effect if my msvcr100.dll is remove from my system32???
Will my computer be broken or something???
Will my computer be slow???
what if I edited it for example I replace my original msvcr100.dll that has a size of 752b to 732b or vice versa...
ASAP!!!...
Thanks for the tip! Your instructions are extremely well-written.
It's a joy to read instructions that actually include all of the steps, unlike most of the Java how-to's I've found.
Well, this would be neat if it worked but I get errors such as:
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "void __cdecl std::_Xlength_error(char const *)" (?_Xlength_error@std@@YAXPBD@Z) already defined in libcpmt.lib(xthrow.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "void __cdecl std::_Xout_of_range(char const *)" (?_Xout_of_range@std@@YAXPBD@Z) already defined in libcpmt.lib(xthrow.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "public: virtual __thiscall std::basic_streambuf<char,struct std::char_traits >::~basic_streambuf<char,struct std::char_traits >(void)" (??1?$basic_streambuf@DU?$char_traits@D@std@@@std@@UAE@XZ) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "protected: __thiscall std::basic_streambuf<char,struct std::char_traits >::basic_streambuf<char,struct std::char_traits >(void)" (??0?$basic_streambuf@DU?$char_traits@D@std@@@std@@IAE@XZ) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "protected: char * __thiscall std::basic_streambuf<char,struct std::char_traits >::pptr(void)const " (?pptr@?$basic_streambuf@DU?$char_traits@D@std@@@std@@IBEPADXZ) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "protected: char * __thiscall std::basic_streambuf<char,struct std::char_traits >::gptr(void)const " (?gptr@?$basic_streambuf@DU?$char_traits@D@std@@@std@@IBEPADXZ) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "protected: void __thiscall std::basic_streambuf<char,struct std::char_traits >::pbump(int)" (?pbump@?$basic_streambuf@DU?$char_traits@D@std@@@std@@IAEXH@Z) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "protected: void __thiscall std::basic_streambuf<char,struct std::char_traits >::gbump(int)" (?gbump@?$basic_streambuf@DU?$char_traits@D@std@@@std@@IAEXH@Z) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "protected: char * __thiscall std::basic_streambuf<char,struct std::char_traits >::_Pninc(void)" (?_Pninc@?$basic_streambuf@DU?$char_traits@D@std@@@std@@IAEPADXZ) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "public: void __thiscall std::basic_ios<char,struct std::char_traits >::setstate(int,bool)" (?setstate@?$basic_ios@DU?$char_traits@D@std@@@std@@QAEXH_N@Z) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "public: virtual __thiscall std::basic_ostream<char,struct std::char_traits >::~basic_ostream<char,struct std::char_traits >(void)" (??1?$basic_ostream@DU?$char_traits@D@std@@@std@@UAE@XZ) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "public: virtual __thiscall std::basic_ios<char,struct std::char_traits >::~basic_ios<char,struct std::char_traits >(void)" (??1?$basic_ios@DU?$char_traits@D@std@@@std@@UAE@XZ) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "public: __thiscall std::basic_ostream<char,struct std::char_traits >::basic_ostream<char,struct std::char_traits >(class std::basic_streambuf<char,struct std::char_traits > *,bool)" (??0?$basic_ostream@DU?$char_traits@D@std@@@std@@QAE@PAV?$basic_streambuf@DU?$char_traits@D@std@@@1@_N@Z) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "protected: __thiscall std::basic_ios<char,struct std::char_traits >::basic_ios<char,struct std::char_traits >(void)" (??0?$basic_ios@DU?$char_traits@D@std@@@std@@IAE@XZ) already defined in libcpmt.lib(cout.obj)
1>msvcprt.lib(MSVCP100.dll) : error LNK2005: "public: void __thiscall std::basic_ios<char,struct std::char_traits >::clear(int,bool)" (?clear@?$basic_ios@DU?$char_traits@D@std@@@std@@QAEXH_N@Z) already defined in libcpmt.lib(cout.obj)
when compiling with /MT.
Any idea?
Everything says it is already defined. You must have an unrelated issue.
no i get this exact same error when setting debug instead of debug dll. this IS related. i have no idea what the problem is.
You can ignore one of the libs in the library config options or set the option to allow for multiple defined symbols
thanks for helping me out i really needed this i was looking all over the internet and u are the only one who helped me 🙂
Greetings, Darren
Yeah...same thing when I was first looking for this. The information was there, but wasn't clear or well-written. Hopefully my post is both clear and well-written.
Thanks, well written and it solved same issue I was having.
thank you for saving my time mate!
Glad to help.
Thanks a ton!